Meddrag – Tradisjonelt bygghandverk

Erfaring frå novhogging av rått virke med mé og maur som oppmerkingsverktøy

Røynsler og ettertanke frå novhogging av rått virke med mé og maur som oppmerkingsverktøy

I dette blogginnlegget visar eg fleire gonger til ei bacheloroppgåve av Selsjord, Høgnes og Aabol, 2022 NTNU. Nokre gonger nemnt her som “bacheloroppgåva”. Eg visar òg til Om Det å Lafte, band 2. Godal, J. B. Olstad, H og Moldal, S. 2018 Fagbokforlaget.

Litt om det praktiske utgangspunktet

Byggeprosjektet som har gitt anledning til å røyne og reflektere over dette emnet er ein tilnærma kopi av eit hønsehus som står på Haverstad i Sør-Fron kommune.

Bilde av referansebygget «hønsehuset» slik det står

Mesteparten av det gjenbrukte tømmeret (frå tredje kvarv og opp) er antatt å stamme frå eitt eller fleire andre bygg som utfrå novskalleform og smekre dimensjonar kan sjå ut til å vere opprinneleg oppført på siste halvdel av 1800-talet (etter samtale med Aabol).

Dei første to kvarva er av annan kvalitet enn resten, har ikkje tilforma novskallar, og har reint barkelaft med rett barke, saga. Så denne delen har eg antatt å vere frå første halvdel av 1900-talet. Stavkonstruksjonen som utgjer andre etasje ser òg ut til å vere frå 1900-talet.

Bilde av kopien under tilvirking

Ein tilnærma kopi av hønsehuset: Vi har hatt visse fridomar i utføringa og tilpassing for ny bruk. Dei første to kvarva vart rydd og hogd, men i same dimensjon og med same barke som på referansebygget. Vi har derfor også fått anledning til å prøve ut oppmerkingsverktøy ulike tilnærmingar i tømringa av dette bygget. Her står huset snart klart for heil lengde over dør og vindaugsopningar.

Et bilde som inneholder sko, snø, grunn, person

Automatisk generert beskrivelse

Mé og maur

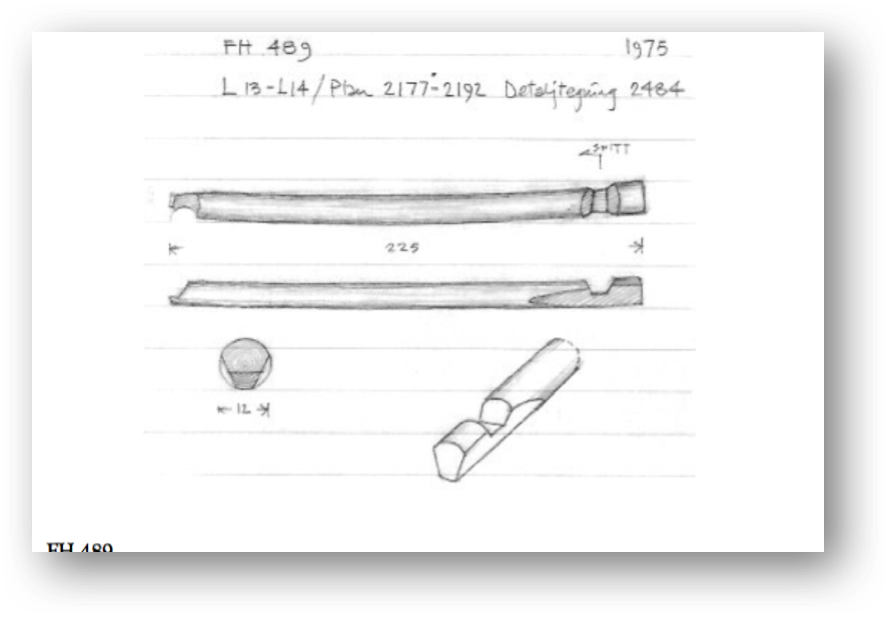
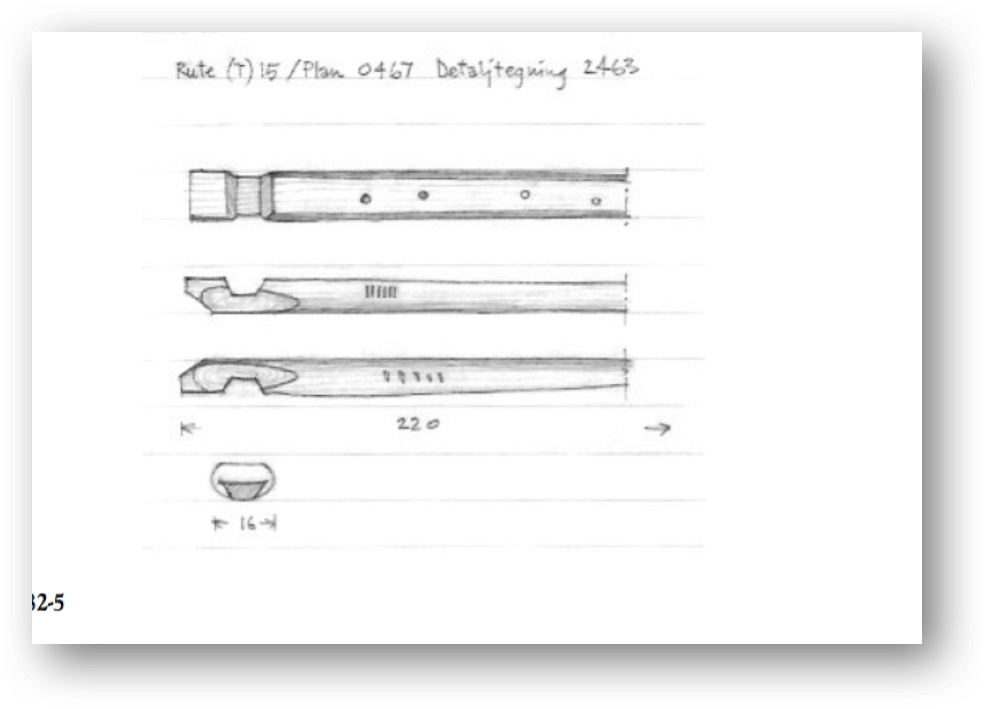
For å hogge saman novene har vi brukt mé og maur til å merke. Akkurat dette dømet på mé- og maurdrag kjem frå ein original som har sitt opphav i Melhus ifølge auksjonisten som solgte han til Roald Renmælmo, og formen er ifølge sistnemnde ikkje uvanleg å finne vidare i Trøndelag og Nord-Gudbrandsdalen. Kopien vi brukte er smidd av Pål Lien.

Rått virke og heng

Vi tok i bruk mé og maur til å lafte, og etter noko utprøving i starten, falt vi på forholdet mellom liten maur til laftet og stor mé til méfaret.

I mm svarar dette til

liten maur: 6 mm (ca ¼ tomme)

stor mé: 24 mm (ca 7/8 tomme)

Kinningsfallet på tømra vår varierte mellom 50-68 grader. Dette ga oss eit heng på gjennomsnittleg 6 mm, eller ¼’’, som vi med rettleiarane vurderte til passande heng for å lafte med den dimensjonen tømmer, 6’’sidetelja og opp til 12’’ høgde, som kom rått frå skogen utan å ha lege til tørk. På eit anna bygg på læringsarena, hadde vi større rundtømmer opp til 20’’. Her var henget vald til 12 mm , eller ½ ’’, grunna meir eigenvekt, og truleg meir romfangsendring i samsvar med større dimensjonar.

Et bilde som inneholder tømmer, tre, Planke, Tømmerhogst

Automatisk generert beskrivelse

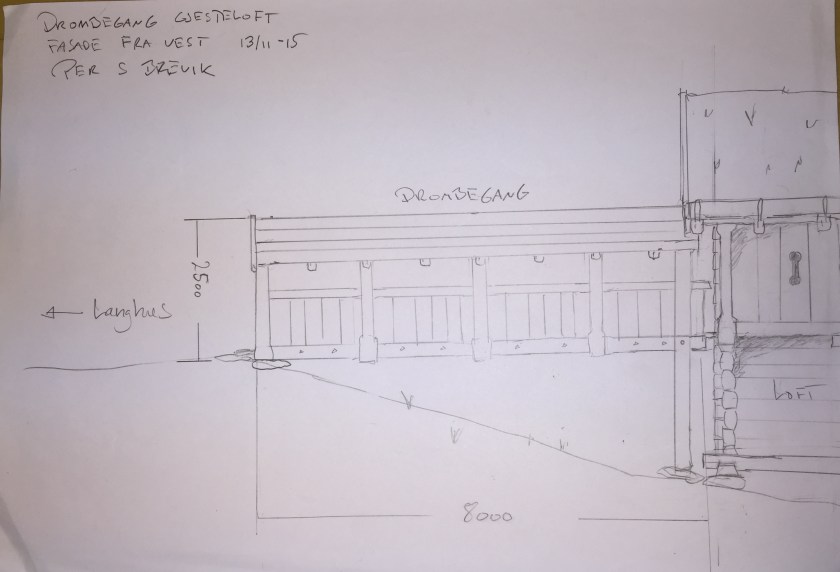
Kopi av stallen frå Haugøy med 1/2» (12 mm) heng

Etter kvart som våren kjem og vi held fram med å lafte, vil tømmeret naturlegvis vere meir tørt og allereie ha krympa noko. Til det kjem vurderinga om å knipe inn henget utover i sesongen. Men kanskje også taklasten ville få bygget til å gå nok i saman. Vekta frå stokkane over ein gitt stokk, blir òg lågare jo høgare opp i bygget ein kjem. Så her er fleire argument for å redusere henget jo lenger opp ein kjem, og etter kvart som tømmeret tørkar.

Sidetelja tømmer med heng. Den øverste rundstokken ligg på i midten, av eigen vekt.

Nærbilde av 1/4» (6mm) heng.

Cosinus og invertert cosinus – korleis fungerer mauringa?

På byggeplass er det kanskje ikkje nødvendig å gjere nokre fleire utrekningar enn berre å prøve seg fram til ønska heng, der justerar ein det på skjønn utfrå erfaring. Det oppstod for min del ein trong til for å forstå kva som ligg i å maure. Det finst noko lesestoff som kan hjelpe til i forståinga av oppmerkingsreiskapen mé og maur. I bacheloroppgåva Høgnes, Aabol, Selsjord, NTNU 2022, visast det blant anna til tabellane i Om Det å Lafte band 2, s 102.

Etter første gjennomlesing av tabellane i Om Det å Lafte band 2, s 102, oppnådde eg ikkje tilfredsstillande innsikt. Og etter å ha komme tilbake til problemet fleire gonger, har eg gjort eit forsøk på å finne ein logikk som gjev meining for meg. Eg vil dele noko av denne prosessen her, då eg håpar det kan vere nyttig for andre som er på same søken.

Her er eit utsnitt av tabellane i Om Det å Lafte band 2, s 102, med ei lita omstokking av innhaldet, og med kommentarar/gjennomgang i dei svarte bolkane. Det kan vere nyttig å lese heile kapittelet desse tabellane er ein del av.

For å bryte det ned kan det vere greitt å sjå litt på trigonometri. Her er eit forsøk på ein gjennomgang som vonleg vil gjere det enkelt å forstå:

Utan verdiar innslått er

Cos = 1

Cos⁻¹ = 90°

Her er ein enkel framgangsmåte for å finne det kinningsfallet som mé og maur svarar til:

mé / maur = x

1 / x = y

Cos−1 (y) ≈ kinningsfall

Først reknar ein ut kva for tal ein får om ein deler mébreidda på maurbreidda:

Td. 24 / 6 = 4

Så deler ein 1 på det talet og får eit desimaltal

Td. 1/4 = 0,25

Så trykkar ein inn på kalkulator: invertert cosinus og desimaltalet.

Td. Cos−1 (0,25) ≈ 76

76 grader er kinningsfallet.

Desse tabellane visar ein teoretisk samanheng mellom mé og maur som svarar til eit kinningsfall. Dei tek ikkje omsyn til heng.

Det er fleire andre omsyn å ta ved justering av kinningsfall til å passe eit mé- og maurdrag. Og det kinningsfallet som er teoretisk rett for ein viss kombinasjon mé- og maurbreidde, er ikkje nødvendigvis det ein ønskar å bruke. Om virket er rått, sig i bygget frå eigen vekt og taklast spelar inn.

Med kalkulator tek vi moderne hjelpemiddel i bruk og eg har ikkje klart å komme fram til ein enklare måte å rekne ut kinningsfallet ifrå eit forhald mé- og maurbreidde, ved hjelp av hovudrekning. Våre forgjengarar som lafta hadde ikkje moderne kalkulator i lomma, og kanskje ikkje kunnskapen til å rekne trigonometri, utan at eg vil anta noko om kva dei visste og ikkje visste. Uansett meiner eg at fortidas utstrakte bruk av mé og maur synar, om ikkje ei uttalt så, ei ibuande forståing av trigonometri i tillegg til ei solid forståing av det levande materialet og bygningsmekanikk.

Kvifor gjere det meir vanskeleg enn å overføre loddet med passar? Eg trur det er fordi maur er overlegent til å merke opp, då den kan ligge an på kinninga heilt inntil underhogget som skal rissast opp, og framleis gir eit godt resultat innanfor eit spenn av kinningsfall. Den tek opp ujamnskapar i kinningsflata.

I praksis viser det seg at det ikkje er nødvendig å ha kjennskap til matematikken bak. Og når vi kjem til å lafte med heng og å lafte med rått virke, blir det i mi oppleving at å røyne seg fram og eventuelt justere mé- og maurbreiddene ein god veg til målet. Og sidan ein uansett vil få ein viss grad av kompresjon i laftet, og sig i bygget, blir det ein skjønnsmessig vurdering uavhengig av trigonometrien, på kva som blir rett kinningsfall eller høve mé/maur i kvart tilfelle.

Justeringar for å oppnå ønska heng

Det er to måtar vi på læringsarena fann at kan hjelpe oss å justere henget når ein laftar med mé og maur:

Den eine er å endre maur- og mébreidda, den andre er å justere fallet på kinningane.

Eit mé- og maurdrag har ofte to maurdrag og to médrag. På læringsarena Innlandet bruka vi mé og maurdrag som hadde desse måla:

maur: lita opning 1/4» (6 mm) og stor 1/2» (12 mm);

mé: lita opning 11/16» (18 mm) og stor 15/16 (24 mm)

Utan å tenke på heng svarar gjennom tabellformelen liten maur og lita mé til kinning på 70°.

Stor mé og maur gir 75°. Det blir relativt bratte kinningar. Gitt at ein har nøyaktig dette kinningsfallet vil stokken ifølge tabellen ligge på både i nov og mefar når han er ferdig hogd. Brattleik, romfangsendring og vekt vil gi utslag ved at stokken fell saman eit stykke i nova, legg seg på mefaret og på sikt blir utett mellom underhogg og kinning. Derfor er det ein god idé at anten kinningsfallet er lågare eller at det er mellomrom til méfaret, slik at stokken har anledning til å komme ned ein viss mengde i laftet, utan at méfaret (resten av stokken) hindrar det.

Det er her ein, i mi forståing, ser at ein ikkje har eller kan ha eit fasitsvar på kva som er rett forhold mellom mé og maur. Gitt at den mengda stokken vil komme ned i laftet kan ha med mange faktorar å gjere, igjen; brattleik, romfangsendring og vekt – og kanskje også særvekt i tørrstoffet.

I tillegg vil brattare kinning gi meir sig og slakare kinning mindre. Så dersom ein nyttar same maur i rot som i topp, kan ein etter kvart få eit avvik på ønska heng, der det på grunn av slakare kinning i toppen ikke blir hogd ut nok i nova, og i tillegg sig mindre når det kjem vekt på. Om dette er eit forløp som jamnar seg ut når taklasta kjem på, er framleis et spørsmål for meg.

-Sjølv hellar eg litt mot å tru at det ikkje jamnar seg ut, men at henget bør vere likt langs heile mefaret, eller viss noko, vere litt mindre mot nova som har slake kinningar fordi her vil det antakeleg falle mindre saman i laftet. For å oppnå det, kan ein ofte ikkje bruke same maur på nova i rota som den i toppen.

Det førre avsnittet prøvar å støtte opp argumentet om at det kan ha blitt bruka liten maur på oppsåte rot og stor maur på oppsåte topp, slik som vart nemnt av tradisjonsberar Oddbjørn Myrdal: “Langsmed kinningene ble den andre enden brukt (maurene). Disse hadde forskjellig bredde og den smale ble brukt i rota der kinningene var brattere og den brede ble brukt i toppen der kinningen var slakere. Og det vart da tett sånn” i samtale med Hans Høgnes, gjengitt i Hans sin del av bacheloppgåva s. 62.

Det å bruke liten maur til høg oppsåte og stor maur til låg, kan kanskje gjelde mest ved lange lengder og stor avsmalning. Om maurane vart tenkt brukt til dette formålet, er ikkje godt å seie, – men at det mogleg synast eg er verdt å merke seg.

Praksis på læringsarena

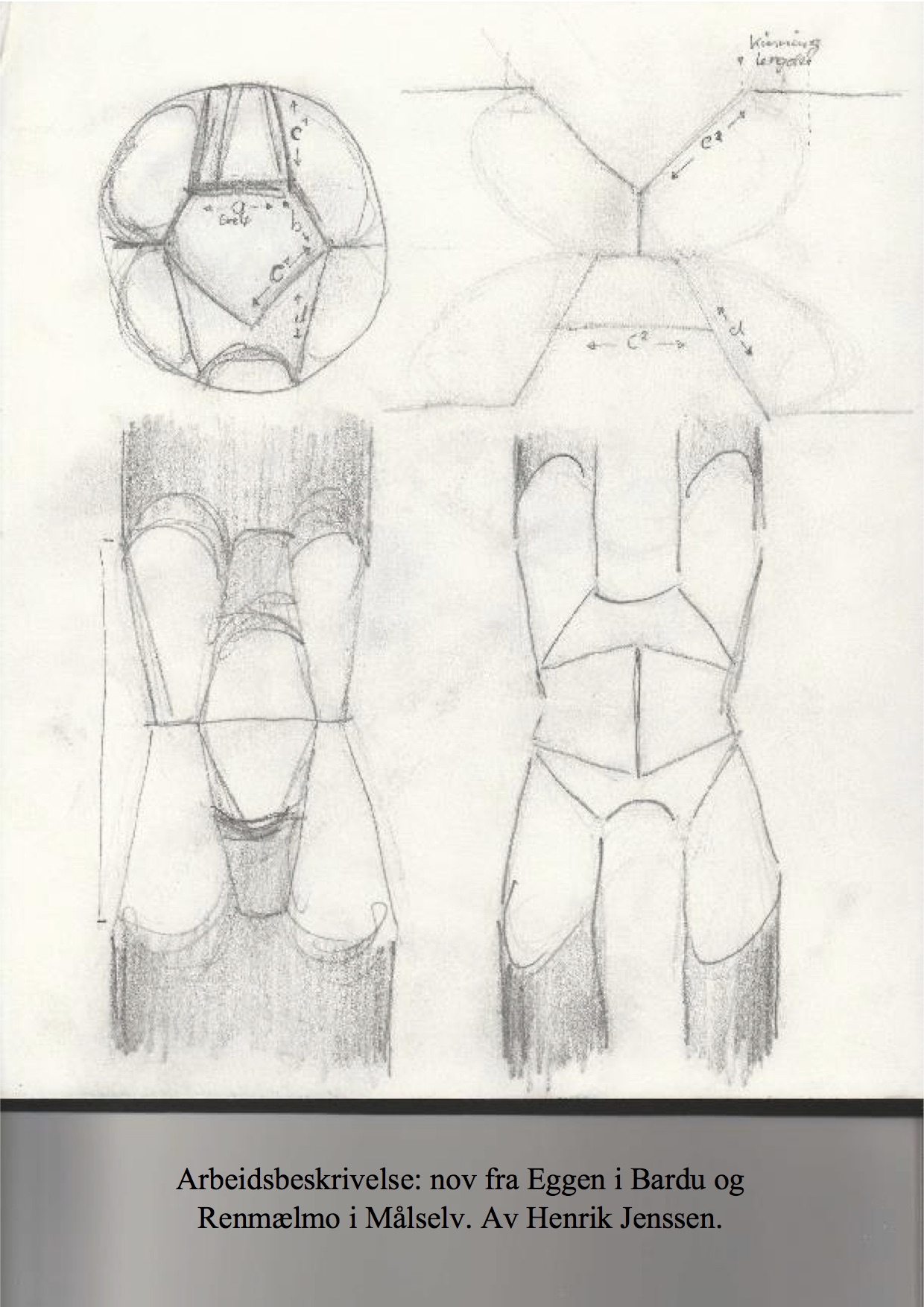
Slik novhogginga på kopien av hønsehuset på Haverstad ble utført, hadde vi i grunn to parametrar å forhalde oss til som avgjorde kinningsfallet.

Det eine var ønsket om at mefaret (og dermed kinning på underhogget) skulle treffe omtrent der kinninga på oppsåta botna, men også slik at øverst på kinninga til stokken som låg parallelt under også traff omtrent på nemnte plass, slik at det ikkje kunne komme glipe i møtet mellom méfar og nov.

Bilde av at underkinning, botn kinning og topp kinning treffast

Dette vart avgjort med to faste mål:

–Den faste dimensjonen gjennom nova , i dette tilfellet 6”

–Og méfarsbreidda, i dette tilfellet omtrent 1/3-1/2 dimensjon (eller der topp kinning råka dimensjonen).

Og det andre som gjorde at kinningsfallet varierte på hønsehuskopien, var høgda på stokken. Frå rot til topp kan kinningsfallet endre seg såpass at det vart synleg meir heng i toppen der det blei lågare kinningsfall. Her spelte avsmalinga på stokken inn. Ein hadde litt slingringsmonn på utforminga til kinninga ved at ein kunne trekke toppen av kinninga lenger ut eller inn frå vegglivet. Dette kunne føre til at når ein médrog méfaret til påstokken ville den kunne treffe nede i kinningsflata på stokken under. Dét igjen kunne motverkast ved at ein lot det vere litt smalare méfar ut mot den enden. Men i fleire eldre bygg vi har sett på har dei ikkje alltid tatt omsyn til det, og det er glipe inn i méfar der han møtar kinning på stokken under.

Det vart fleire små knep og justeringar ein lærte seg undervegs på læringsarenaen, og som rettleiarane kunne dele med oss. I referansebygg ser ein ofte at méfarsbreidda varierar men held seg rundt nokonlunde faste mål, og ein kan fabulere om at lafterane i X tidsperiode har gjort same røynsle og stod i tilsvarande utfordringar som vi har gjort i denne perioden.

I samtale med John Ola Selsjord kunne vi også underholde tanken om at maur og mé vart justert etter slik huset, eller stokkane ville at det skulle vere, og at laftarane kunne kaldsmi sine médrags- og maurjern på byggeplass etter slik dei ville ha måla. Om ein hadde ein dimensjon som ikkje var tilpassa sitt merkeverktøy, vart kanskje det mest effektive å justere han.

Når ein skal gjere justeringar for å oppnå optimalt heng for at det skal sige tett i nova og samstundes bli tett i måsafaret, er det dei ukjente faktorane om korleis stokken oppførar seg medan det tørker og får vekt ovanfrå og kva utslag dei vil gje som fordrar ein skjønnsmessig vurdering. Og sjølv om vi kanskje ikkje er klokare på nøyaktig korleis dei forskjellige tømrarane gjorde det i si tid, kunne vi komme fram til meir eller mindre tilfredsstillande resultat i forsøka våre. Når bygget får stått med taklast og sig på plass, får vi sjå om vi har truffe rett.

Drombe på Stiklastadir, endelig ferdig og i bruk.

I 2016 skrev kollega på Stiklestad Nasjonale Kultursenter Kai Johansen på denne bloggen om Drombegang på gjesteloftet Stiklastadir. Dromben, eller drumben som det også skrives, blant annet i kilder fra Valle, stod ferdig nå i juni til sesongåpning, og jeg tenkte å skrive en kort oppsummering av sluttspurten og vise noen bilder av resultatet, med særlig vekt på taket.

Det tok litt tid fra de første skissene jeg tegnet i november 2015:

Men når jeg nå hentet de fram igjen, så ser jeg at resultatet har blitt nokså likt de ideene vi hadde etter en del undersøkelser og planlegging som Kai skrev en del om i sitt innlegg.

En forskjell er at vi valgte å lukke den mer enn opprinnelig tenkt. Veggtilene går helt opp i stavlina, og det er kun glugger i veggen. Dette gjorde vi først og fremst for å skjerme mer mot snø og regn, da det blåser nokså godt mellom husene her oppe på bakken. Vi valgte også å stø den på midten med to staver under svillene, da vi så at 8 meter uten understøtting nok var i lengste laget. Vi hadde opprinnelig også tenkt å unngå å forankre dromben direkte i loftet, men la den stå på egne staver inne ved loftet. Dette gikk vi bort fra og den er nå felt inn i nova og novarma på loftet. Novarma ble forsterket med en stav under ned til svill på sval i første etasje.

Omtrent halvparten av materialene til dromben er bearbeidet for hand fra rund stokk, enten gjennom kløyving, som veggtiler og takbord, eller hogd til fasong, som syll, staver og mønekjøl.

Både Kai Johansen og Roald Renmælmo har skrevet om kløyving og kløyveforsøk vi gjorde i forbindelse med dette i egne innlegg:

Kløyving av tømmer, tradisjonelle metoder og eksperimentelle forsøk

Kløyving av tømmer, utprøving av ulike prinsipp basert på tradisjon

Over er noe av prosessen med å hogge mønekjølen. Den er hogd av ett emne, 8 meter lang. Og den passet på taket til slutt 🙂

Takkonstruksjonen på dromben er inspirert av takkonstruksjoner fra stavkirker, særlig Haltdalen. Sutaket er bord formet og medratt til hverandre, og skjøtet med en skrå skåring med dreneringsrenne i. Taket ble bygget flatt på en rigg som tilsvarte sperrene i drumben, og så demontert og flyttet ut.

Sperrene på plass, nå mangler bare taket. For å å få litt mer stabilitet valgte vi å lage annenhver sperre med ei saksesperre i.

Taket legges. Vi valgte å spikre taket med 4″ smidd spiker, mest fordi vi syntes trenagler ville være litt brutalt i de nokså tynne sperrene.

Takbordene bestod både av kløyvde og sagde bord. Her merket vi oss at de kløyvde bordene nok var noe mer stabile i formen, men det var ikke uten unntak. En del både kløyvd og sagd material var såpass tvinnet at det var tilnærmet uråd å bruke.

Den fremste sperra har et rotkne festet foran som en sperre og «portal» Dette for å stive av dromben sideveis her, samtidig som vi får god høyde i inngangen. Det er hogd dørfals i søylene i portalen, i tilfelle vi skulle få lyst til å bygge flere middelalderdører.

Golvet har skjøt midt i dromben, og består av halvkløyvinger. Noen ble litt for granne, og må skiftes. Ellers ble det et stødig golv.

Endelig er dromben på plass! Vi er ganske godt nøgde, og synes den ble et godt tilskudd til loftet, den vekker oppmerksomhet hos publikum og er god å formidle byggeteknikk og takkontruksjon med. Og ikke minst gir den oss en unisversell, stilfull og stødig adkomst til loftet for alle.

Ei enkel mellomaldernov? Forsøk på å rekonstruere ein framgangsmåte for ei 1000 år gammal nov frå Nidaros

Våren 2016 vart Jon Godal, Harald Høgseth og eg invitert ein tur til Vitenskapsmuseet i Trondheim av Karin Rosberg, ein svensk arkitekt som forskar på vikingtidas byggeskikk i Mälardalen. Vi var der av di Karin Rosberg ønskte hjelp til å synfare nokre utvalde stokkar frå den eldste byoppkomsten i Trondheim, i hovudsak 1000-talet, og fleire å diskutere med når ho skulle sjå på desse bygningsrestane frå tidleg mellomalder.

Karin hadde valt ut nokre av dei stokkane som vart tekne vare på og konservert etter gravingar i mellomalderens kulturlag i Trondheim på 1970-talet. Eg tenkte at i tillegg til å kunne diskutere problemstillingane Karin ynskte å ta opp, var dette og ein fin anledning for å kunne sjå litt nærare på noko av det eldste vi har bevart av tømra nover her til lands.

Eg skulle skrive blogginnlegg om dette rett etterpå, men det blei ikkje gjort. Så no har eg nytta høvet og endeleg fått gjort ferdig ei lita utgreiing om noko av det vi såg på, og mitt forsøk på å rekonstruere ein framgangsmåte for novene vi har bevart frå Nidaros eldste bygningshistorie.

Om nova og bakgrunnen for å velje denne.

Under arkeologiske utgravingar i Trondheim på 1970 talet ble det funne mange til dels godt bevarte bygningsdelar i tre. Dei eldste er heilt frå tida då byen vaks fram mot slutten av 900-talet, og det er grave fram mengder av treverk frå heile mellomalderen. For det meste dreier det seg om dei nedste delane av bygningar eller andre konstruksjonar, som syllstokkar, golvåsar, golvbord, kavlebruer, fundamentstabbar, gjerdepålar, bryggepålar og liknande. Nokre av desse er veggstokkar med bevarte detaljar som kan seie noko om korleis ein tømra husa på Nidarneset for 1000 år sidan. Mykje av materialet blei ikkje teke vare på, av omsyn til lagringsplass og kostnader ved konservering, så det er berre eit utval som vi i dag kan studere nærare.

Frå det materialet Karin såg på, har eg valt ut ei nov som eg har prøvd meg på å rekonstruere. Det er ei underhalsnov, som har lange halsingar som går til enden av stokken (fig. 1). Nova blir kalla rännknut på svensk, og er vanleg i bygg frå mellomalder blant anna i Dälarna (fig. 4 og 5) Nova er og i slekt med findalsnova, som kanskje kan seies å vere ein avansert vidareutvikling av denne enkle underhalsnova.

Gjennom arbeidet med å tømre gjesteloftet på Mellomaldergarden Stiklastadir ved Stiklestad Nasjonale Kultursenter, har eg fått auka interesse for dei eldste novformane vi kjenner her i landet, og eg tenkte det kunne vere interessant å forsøke å rekonstruere ei av desse og berre nytte verkty som var tilgjengelege for tømraren i mellomalderen.

figur1 — Figur 1: Teikning av stokk, frå utgraving på Folkebibliotekstomta i Trondheim i 1975. Her er lite detaljar, men vi ser at det dreier seg om ei underhalsnov, med lang halsing som går heilt ut til stokkenden. Stokken er frå åra 1050-1100.

Truleg er denne underhalsnova i ulike variantar ein svær gammal form. Arne Berg viser til at liknande novhogg er funnen frå 300 f.Kr i et gravkammer i Altaifjella i Vest-Sibir.

Ein annan stokk vi såg på hadde ein kortare halsing som ikkje gjekk ut til stokkenden (fig. 2). Det er nok lite som skil framgangsmåten på desse to ulike novene. Eg har valt å tømre den med lange halsingar ut til stokkenden.

Begge stokkane er i små dimensjonar, berre ikring 12 og 16 cm i tverrmål. Eg veit ikkje om desse små dimensjonane er representative for ein større del av materialet frå mellomalderens Nidaros. Men vi kjenner at det ofte er nytta nokså granne stokkar òg i dei bygga, for det meste loft, som enno står att frå mellomalderen i andre strok av landet. Men desse er tømra i furu, medan gran ofte vert nytta i Nidaros. I følgje Høgseth var oppimot 80 % av veggtømmeret i høgmellomalderen gran.

figur2 — Figur 2: Underhalsnov med halsing som ikkje går heilt ut til enden. Stokken har vore bruka opp att fleire gonger. Den har to nummereringar, 5 og 6, og har truleg til slut enda opp som golvås. Da har den fått flathoggen overside og hol for etter det som kan ha vore pluggar for å festa golvborda. Stokken er funnen under graving i Kjøpmannsgata i Trondheim i 1971, i lag som dateras til 1150-1250. Den ble funnen under golvet i det som truleg var restane etter ei årestue.

figur3 — Figur 3: Stokk T82-5, same som på skissa over frå 1971. Vi kan sjå halsingen og overhogget. øksespora er enno tydelege både i sidene og botnen i hogget. Det var ikkje lett å sjå sikre spor etter lengda på eggen på øksa som er nytta, men det ser ut til å kunne vere ei øks med ein egglengde på ikring 6-9cm.

Figur 4: Rännknut i härbre, datert 1285, i Älvdalen Sverige.

ra%cc%88nnknut-i-ra%cc%88ttvik-dalarna — Figur 5: Rännknut i ei løe, truleg 1200-tal, i Rättvik Sverige

Arbeidsbeskrivelse:

Eg valde å tømre prøvenova i gran. Originalen er eg usikker på om er i gran eller furu, det er muleg at det er gran. Som nemnt er det funnen rett mykje gran som veggtømmer i Trondheims mellomalderhus. Det er heller ikkje viktig i denne samanheng for mitt forsøk, om eg tømrar i gran eller furu.

Mitt korte ”teoretiske utgangspunkt” er at eg trur tømrarane i mellomalderen ikkje merka opp rett mykje under prosessen, men at det meste gjekk på augemål, erfaring, og nokre få hjelpemidlar (som loddefjøl og passar eller skrape). Eg har ikkje så rett gale augemål, men det kanskje viktigaste, erfaringa, er det så som så med. Så utgangspunktet er vel ikkje heilt optimalt.

Eg valte meg ut først ut fire korte stokkar som var ikring 20-25 cm i tverrmål. Altså noko større enn dei originale. Eg byrja med å barke og pjåle stokkane. Eg valde å pjåle dei, sjølv om eg ikkje kunne sjå sikre spor etter kva verkty dei var barka og sletta med. Deretter flathogde eg undersida på to stokkar, mest for at dei skulle ligge betre.

Desse stokkane blei lagt ut til syll på kortveggane, og så blei ein lagt ut på tvers over, klar til felling ned i desse (fig. 6).

Sidan dette er første omfar, må eg byrja med å bestemme kor eg vil plassere stokken i høve til stokkenden på den under. Eg valde å legge den slik at novhovudet blir stikkande ei handsbreidd utafor veggen. Eg merker meg så kor midten av stokken eg skal felle ned treff den under, og hogger overhogg som er ein del smalare enn stokkbreidda på den eg skal felle ned. Her kan ein bruke augemål, eller passar som ein sjekkar breidda på stokken med for å sikre at ein ikkje høgg for bredt overhogg.

figur4 — Figur 6:To stokkar er lagt ut til kortveggar, og ein stokk er lagt klar til å byrje hogging.

figur5 — Figur 7: Med skogsøksa hogger eg ut eit overhogg som er noko smalare enn tverrmål på stokken som skal nedi. Her blir det stødig å legge stokken for hogging av halsing.

Så bestemmer eg kva som er rette vegen for stokken som skal felles ned. Eg legg rygg og kuv opp, og merker så opp med loddefjøl i begge endar (fig. 8) Deretter høgg ein halsingane som vist på figur 9.

figur6 — Figur 8: Ein avgjer kva som er opp på stokken (kuv opp), legg den rett og rissar ein loddstrek i kvar ende ved bruk av loddfjøl.

figur7 — Figur 9: Etter at ein har merkt loddet i stokken, snur ein den opp ned og høgg halsingane. Dei høgg ein ned mot halve stokkbreidda. På undersida (opp her) høgg ein slik at det blir att passeleg breidd, omtrent det ein ser for seg skal vere breidda på måddåfaret.

Både halsingar og overhogg prøver eg på sjå for meg skal bli i om lag same vinkel, slik at dei skal falle nokså godt i hop når ein legg nedi for vidare oppmerking (fig. 8).

figur8 — Figur 10: Om ein prøver å hogge vinkel og djupn i halsingar og overhogg like, kan ein vere heldig og dei legg seg fint på plass på for første oppmerking. Enno er det ikkje merkt opp noko anna enn loddline og midten av der ein vil ha overhogget, og elles hogge på augemål.

Eg bruker passar for å merke opp for den vidare hogginga. Eg vil no ha stokken ned hele høgda av halsingen, det vil då seie ikring halve stokkhøgda. Eg tar da høgda med passaren, og bruker denne høgda når eg riper ned halsingen til overhogget (fig. 11-13).

figur9 — Figur 11: På første omfar skal eg felle stokken om lag ned til midt på. Her tar eg høgda med passaren. Eg bruker så den til å medra stokken ned i overhogget.

figur10 — Figur 12: Her ser vi ripmerket etter at passaren er brukt til å ripe ned frå halsingen på stokken over.

figur11 — Figur 13: Så høgg ein etter ripmerket, og håpar ein har klart å bruke passaren stødig og i lodd. No er stokken kome ned dit den skal.

Framgangsmåten når ein går vidare til neste omfar blir temmeleg lik som den over. Men det blir ein operasjon ekstra med nedhogging, da det her blir for mykje å felle den klar til medraging på første hogging. I tillegg skal stokken no médras mot stokken under. Her er framgangsmåte kort skissert for neste omfar:

Som eg har vist over høgg eg først eit overhogg noko mindre enn breidda på stokken som skal nedi.
Stokken som skal felles ned legges slik ein vil ha han i overhogget, den loddes, merkes og leggas opp ned for hogging av halsingar.
Stokken snus, leggas ned i overhogget og ein tar så høgda ned mot stokken under ved nova, og bruker denne som mål når ein no ripar med passaren. Så høgg ein inn til ripa, og stokken skal i teorien falle ned og vere klar til medraging. Kan hende må ein justere og ta litt både i overhogg og mellom stokkane for å få den låg nok til medraging (maks 15-20mm).
Stokken médras med same mål på medrag og passer. Eg brukte eit gamalt medrag eg hadde tilgjengeleg i medraginga mellom stokkane, og passaren til medraging i nova.
Stokken løftast ut att og ein hogger ut etter ripene i måddåfaret og overhogget. Her må ein merke seg at det ikkje må stå att meire enn opp til medragsstreken under halsen på stokken, og at ein høgg overhogget ned til nakken/måsåleggen på stokken under.
Stokken leggas på plass, og passar forhåpentligvis.

Det er heile tida viktig at ein sjekkar at stokken ligg der den skal, både i lodd og at ikkje dei forskyver seg sidevegs. Det lite som låsar i lengda i denne nova, så den kan lett renne av garde. Kanskje ikkje utan grunn at den heiter rännknut på svensk?

figur12 — Figur 14: Fyrste stokken i 2. omfaret er på plass.

Til å tømre denne nova ha eg nytta desse verktya:

kopi av ei lett lita mellomalderøks frå Lierne, Nord-Trøndelag, smidd av Mattias Helje
norsk skogsøks, mellomaldertype, smidd av Bertil Pärmsten
kopi av øks frå ca 1300, funnen i Lödöse, Sverige, smidd av Bertil Pärmsten
passar (frå nyare tid, truleg seint 1800-tal)
medrag
loddfjøl
kniv

Eg kunne godt ha klart meg med berre ei øks, helst ein noko tyngre og litt smalare utgåve av øksa frå Lierne. Og ei skrape hadde nok nytta like godt som passar til å medra novene. Ein god skrap kunne kanskje vore nytta både i nova og mellom stokkane?

I tillegg nytta eg ein bandkniv for å barke tømmeret, og ein pjål frå Jon Dahlmo for å slette tømmeret. Og ei Husqvarna motorsag for kapping…

Erfaringar:

Med litt meir erfaring med denne nova trur eg det skal gå nokså greitt å tømre med den, utan anna verkty enn dei nemnte. Eg vil sjå på forbetringar i val av passar, helst vil eg få smidd meg ein god skrap som eg vil teste ut både i nova og mellom stokkane.

Ei erfaring eg gjorde når eg tok til med 2. omfaret var at eg ikkje var nøye nok med val av stokkar her. Det var for stor skilnad på tverrmålet på den eg skulle felle ned i og den som skulle fellast ned. Det gjer at ein får problem med at overstokken fell for langt ned i stokken under, og problemet forplantar seg vidare. Jamt tømmer og små dimensjonar er ein fordel. Elles meiner eg prosedyren eg såg for meg og no har testa ut så smått ser ut til å kunne fungere.

Nova ser svært enkel ut, om den ikkje er direkte krevjande, så krev ho likevel god planlegging, at ein ser eit godt stykke framfor seg, og helst godt, jamt tømmer, for at dette skal gå greitt og bli bra.

figur13 — Figur 15: Nova opna så ein ser inni.

Sinknov med tapp, i tradisjon etter Arne Pedersen, Aursfjordgård

Tømring av smie med sinknov med Arne Pedersen som læremeister og tradisjonsberar. Foto: Roald Renmælmo

I Desember 2015 fikk jeg en innføring i sinknov med tapp, med Arne Pedersen fra Aursfjord i Troms som tradisjonsbærer. Vi hadde ukene i forkant felt furutømmer og rydd noe av dette til 4 1⁄4″ tykkelse, så tømmeret var ferskt og fint å jobbe med. Bygget er en rekonstruksjon av ei smie tilhørende Aursfjordsaga, så dimensjonene, dør- og vindusplassering er tatt ut i fra det gamle tømmeret. Sinknova med tapp er en av flere nover Pedersen har praktisert gjennom sin tid som tømrer. Den gamle smia kjenner jeg ikke alderen på, men sinknova er kjent for Pedersen.

Størrelsen på bygget kan en merke direkte opp på tømmeret, og vi valgte å gå ut i fra innvendige mål, så gjennom hele prosessen merkes og vatres veggen opp i fra innvendige vegglinjer. Da får en slette vegger innvendig. Syllstokken på langveggen kløyves med sag, en rett og godt utmalma stokk er et fint utgangspunkt. Stokkene i gavlveggene velges ut med omhu, kuven legges opp, og undersiden rys slett. Rotendene legges hver sin vei, overstokkene med rot på understokkens topp. Nå bør en være nøye på at underlaget for syllstokkene er nivellert så alt er i vater. Nå kan Sinknova merkes opp.

Merkeverktøy som blir brukt i tømringa. Foto. Pål Sneve Prestbakk — Merkeverktøy som blir brukt i tømringa. Meddraget er ikke med på bildet. Foto. Pål Sneve Prestbakk

Verktøyet en bruker under merkeprosessen er enkelt, må holdes i god stand og i nærheten. En god og spiss tømrerblyant, en kort og lang vater, en låsbar passer (eller to) og et meddrag. Tommestokk med norske tommer er å foretrekke. Passeren bør kunne svelge unna ca 8 tommer, den lille passeren bruker jeg til å merke høyden på sinken. En stor tømmermannsvinkel er også en del av merkeutstyret.

Høyden på stokken må tas hensyn til når en skal merke størrelsen og plassering av sinken. Som i fig 1, tar vi utgangspunkt i å hugge ut ca 1⁄3 av stokkhøyden, så fremdeles kjernen av stokken kommer ut i enden. Se vaterlinje og sinklinje merket i fig 1.

Fig 1. Skjematisk framstilling av nova. Foto: Pål Sneve Prestbakk

Merking av sink

Overstokkens bredde merkes på understokken, merkes med loddlinjer på sideflatene. På samme vis merkes understokkens bredde på overstokken. Sinkhøyden må nå bestemmes. Vi la opp til 2 cm fall, det stemmer omtrendt med meddragshøyden vi kommer tilbake til. Innvendig og utvendig hjørne på sinken har lik høyde. De to motsatte hjørnene (på de ytre veggflatene) har da totalt 4cm høydeforskjell. Vannet ledes kun ut av veggen, mens sinken gjør nova trangere på innsiden så tømmeret låses.

Overstokken ligger på plass når en merker sinken. (Fig 5.) Det var noe upraktisk for å ta gode bilder, men merkene viser hvor den ligger. Den må være i lodd på innvendig vegg, justert i lik høyde på begge sider, så festes stokken med haldhaker. Loddlinjene trekkes opp på overstokken med vateren. Stikkhøyden tar vi med passer mellom underkant overstokk og overkant understokk. Høyden på passeren viser nå hvor langt ned overstokken skal felles. Siste fintilpassingen tar vi med meddraget senere, så en må stille ned stikkmålet på passeren et par cm.

Nå kan en enkelt merke opp stikkhøyden med passer, og rutinen er å gå rundt nova med sola. Vaterlinjen trekkes ut fra innvendig hjørne, det måles to cm opp, så har en den første sinkflaten. Stikkhøyden på passeren settes i dette punktet, og en fører målet opp på overstokken. Herfra trekkes det vaterlinje til utvendig hjørne, og det måles to cm ned. Dette punktet overføres så ned på understokken med passeren, og det vatres til neste punkt og to cm ned. Til slutt overføres dette punktet opp med passeren og mellom loddlinjene kan en trekke sinklinjer. -innvendig og utvendig hjørne på sinken er da i lik høyde.

Overstokken flyttes til siden og snus opp-ned. Tappen og slissen kan merkes. Tappmerkingen gjør en konsekvent med tappjernet, i dette tilfellet et 7⁄8″ jern. Se ferdig merket syllstokk fig 1. Stikkmålet må også vise hvor dypt tapprommet skal være i overstokken.

Fig 2. Understokken er ferdig med tapp og sliss. Foto: Pål Sneve Prestbakk — Fig 2. Understokken er ferdig med tapp og sliss. Tappjernet brukes for å kontrollere måla på tapp og sliss. Både lengde og bredde på tapp og sliss er tatt ut fra tappjernet på ⅞». Foto: Pål Sneve Prestbakk

Nå kan nova hugges ut, og en starter med å sage ned til sinkhøyden i forkant av tappen, så den blir helt i lodd. Sinkflata hugges ut med ei passelig bile, og tappen renskes opp med tappjern. Tapprommet kan sages på sidene, og tas ut med tappjern. Nå er det fint å sjekke at størrelsen på tapp og sliss stemmer overens, med tappjernet som referanse!

Se ferdig hugget nov og tapper i fig 2. Arne Pedersen fasa også av hjørnene på tappen for at den lettere skal entre i neste stokk. En må huske at tapprommet i overstokken ikke skal gå hele veien. Se merking fig 3. Overstokken er ferdig tappet og klar til første prøve.

Fig 3. Slissen er ferdig tappa. Foto: Pål Sneve Prestbakk — Fig 3. Slissen er ferdig tappa. Dette er en av syllstokkene som er fotografert opp/ned. Foto: Pål Sneve Prestbakk

Overstokken legges på plass, i lodd, nå er det klart for meddrag. Vi kan måle nøyaktig hvor mye stokken må felles ned for å nå samme planet i bunn. Dette målet overfører en på meddraget, og merker sinken rundt hele nova og overkant tapp på understokk. Husk at en nå ikke skal ta mer av understokken, det skal kun overstokken som skal meddras. Om alt går rett, skal nå alle syllstokkene ligge i vater på underlaget.

Videre er prosessen noenlunde lik, men nå må en gjøre utvalg blant det tilgjengelige tømmeret og finne stokker som passer høvelig mot stokken under. Rot på topp, kuven opp, stokken legges i lik stikkhøyde i begge ender. Nå kan en sjekke overstokken om det er justeringer som må gjøres for at den skal komme ned til meddragshøyde. Kvister, kuler og former kan smis til på begge stokkene så det passer best mulig til meddrag.

Stikkhøyden bestemmes og vi må avgjøre hvor sinken skal plasseres. Utgangspunktet er igjen at vi beholder sinken i en tredjedel av stokkens ferdige høyde. Se fig 4. Dette er ikke bare funksjonelt, men også et estetisk grep for å få en viss rytme i novene.

Fig 4. Inndeling av sinken i novene. Foto: Pål Sneve Prestbakk

Fig 5. I figur 5 ser vi topp-enden av overstokken. Den er justert opp i rett høyde og under oppmerking. Bildet viser at sinken blir fint fordelt, og nede til venstre ser en laveste punkt i sinken, to cm under vaterlinja fra forrige punkt. Foto: Pål Sneve Prestbakk

I det innvendige hjørnet må en nå passe på å merke formen på overstokken ned på understokken, avstanden er stikkmålet. Her kommer tappen i det innvendige hjørnet, til motsetning fra syllstokkene. Når det meddras, skal denne komme lavere og tette mot medfaret. Se fig 6. Igjen, i fig 7 ser vi merking tappens høyde på overstokken.

Fig 6. Legg merke til at stikkhøgda er overført frå underkant påstokk til der tappen sluttar. Foto: Pål Sneve Prestbakk

Fig 7. Stikkmålet blir også overført frå overkant av understokken til påstokken for å avgrense høgda på slissen for tappen. Foto: Pål Sneve Prestbakk

Fig 8. I fig 8 ser en stokken nedfelt til meddragshøyde. Her er også siste andledning for å merke for dymling, det gjør en også på innervegg. Foto: Pål Sneve Prestbakk — Fig 8. I fig 8 ser en stokken nedfelt til meddragshøyde. Foto: Pål Sneve Prestbakk

Medraget blir brukt både for å merke opp for medfaret og for å merke opp flata på sinken på påstokken. Også høgdene på slissene som vist på Fig 6 og Fig 7 blir merka opp med medraget under meddraginga. Dymling blir helst merka og sett i før meddraging.

Nov fra Eggen i Bardu og Renmælmo i Målselv

Figur 18. Skisse av nov fra stabburet på Eggen i Bardu. Skisse: Henrik Jenssen

Dette er et forsøk på en detaljert arbeids- og prosedyrebeskrivelse av en type tømring av nov som har vært brukt i Bardu av den første bosettingen som kom fra Østerdalen på slutten av 1700-tallet. Den har også vært brukt i Målselv, mulig tidligere, men i hvert fall fra 1860-tallet fram til slutten av 1800- tallet.

Arbeidsbeskrivelsen bygger videre på arbeid jeg og medstudenter fra Tradisjonelt Bygghandverk på NTNU gjorde på en studiesamling i Målselv. Vi befarte og dokumenterte et stabbur på gården Eggen i Bardu som trolig er et av de eldste byggene i kommunen. Senere prøvetømret vi og forsøkte å rekonstruere arbeidsmetoden av noven, og pjålingen av stokkene.

Siden da har jeg arbeidet videre med prøvetømringen på egenhånd, med innspill fra veileder Roald Renmælmo. Sammen har vi studert et stabbur som står hjemme på gården hvor jeg bor, Renmælmo i Målselv. Dette er nok ikke så gammelt som stabburet på Eggen, og selv om det har ulik dimensjon og utforming på veggstokkene, har det samme typen nov.

Figur 1. Stabburet på Renmælmo i Målselv. Foto: Henrik Jenssen.

Figur 2. Nærbilde av noven på Renmælmo-stabburet. Foto: Henrik Jenssen. — Figur 2. Nærbilde av novene på Renmælmo-stabburet. Foto: Henrik Jenssen.

Figur 3. Viser nordveggen av Renmælmo-stabburet hvor andreetasjen går over til lengre stokker. Foto: Henrik Jenssen

Da vi studerte stabburet oppdaget Roald et interessant uthogg av en flate på oversiden av de nederste veggstokkene på langveggen i andreetasjen. Han trodde dette kunne peke mot fremgangsmåten som var brukt for å tømre noven. Stabburet har en lengre tømmerdel i andreetasjen og det var på oversiden av de to første stokkene som får full lengde at det var hugget ut en flate. Roald mente det kunne være et merke etter et tidlig steg i prosessen av å hugge noven som her var blitt bevart fordi neste nov ikke kom over den forrige, men lenger ut.

Figur 4. Innsiden av nordveggen i andreetasjen. Foto: Henrik Jenssen

Figur 5. Nærbilde av den uthugde flaten på nordveggen. Foto: Henrik Jenssen.

Vi så også spor etter bruk av meddrag i noen nover, og har derfor også brukt dette som et innspill til arbeidsprosedyren.

Denne teorien har jeg bygget videre på mens jeg har prøvetømret på egenhånd og jeg synes jeg nå har kommet fram til en brukbar teori på hvordan noven kan ha vært tømret, og hvordan den uthugde flaten på Renmælmo-stabburet kan ha havnet der. Arbeidsbeskrivelsen bygger ikke på kunnskap som kommer direkte fra noen tradisjonsbærer.

Figur 6a. Til venstre: nærbilde av spor etter meddrag i nov på Renmælmo-stabburet. Til høyre: nærbilde av øksehogg i medfaret. Foto: Henrik Jenssen

Figur 6b. Til venstre: nærbilde av spor etter meddrag i nov på Renmælmo-stabburet. Til høyre: nærbilde av øksehogg i medfaret. Foto: Henrik Jenssen

Når en veggstokk skal pjåles slik som på stabburet på Eggen er tømmeret som skal brukes så rett og jamnvokst at det er forholdsvis lite som trengs å gjøres. Barken fjernes med pjålen, og grove ujevnheter slettes. På de korte stokk-lengdene jeg prøvetømret med var dette et mindre problem enn det vil kunne være på fulle lengder, men jeg og medstudentene mine observerte at tømmeret på stabburet var svært lite bearbeidet i veden og det var lite fiberbrudd. Dette stiller store krav til hugging av tømmer.

Figur 7. Pjåling av veggtømmer. Foto: Henrik Jenssen.

Når en begynner å tømre legges syllstokkene opp i vater og roskakken (diagonalen) justeres rett. Disse hugges som andre stokker i noven, men det er ingen stokk under som det skal meddrages mot. Et par av de fire syllstokkene må enten være kløyvd til halv høyde, eller så kan det være ujamn grunnflate. Fra nå av beskriver jeg tømringen av en generell veggstokk.

Figur 8. Nærbilde av den uthugde flaten jeg har valgt å kalle "liggeflaten". Foto: Henrik Jenssen — Figur 8. Nærbilde av den uthugde flaten jeg har valgt å kalle «liggeflaten». Foto: Henrik Jenssen

En begynner med å hugge ut «liggeflaten» (som jeg har valgt å kalle den uthugde flaten fra Renmælmo-stabburet) der hvor neste stokk skal komme over. Hvis det er en stokk under siktes det ned mot denne sånn at midten av «liggeflaten» kommer ca. midt over stokken under, men det er viktig å huske på at det til syvende og sist er innerveggen som skal bli i lodd. Dette finjusteres med øyemål underveis i hele prosessen, og vatres helt presist rett før en meddrar. Det er ikke viktig å få «liggeflaten» veldig presis og fin, men det er viktig at flaten og skråsidene er litt kortere enn stokken over er brei ved noven og at flaten er så mye i vater som mulig. Øyemål bør holde. Vinkelen på sidene ned til flaten kan være rundt 45 grader, men det er ikke veldig nøye. Det er viktig at de er vinkelrett med stokken. Dette vil hjelpe med å få vinkelen på neste stokk rett.

Så legges overstokken slik at den hviler på «liggeflaten» på begge understokkene. Den vil rulle en del på dette punktet, men det er ikke et problem. Derimot er det viktig at stokken ligger med kuven opp, hvis den har en, at det er 90 graders vinkel i hjørnene, og at utstikket av stokkene i novene er litt lengre enn veggtykkelsen på tømmeret.

Figur 9. Her er det hugget ut en "liggeflate" i over- og understokken slik at de kan ligge stabilt mot hverandre mens noven på overstokken hugges. Foto: Henrik Jenssen. — Figur 9. Her er det hugget ut en «liggeflate» i over- og understokken slik at de kan ligge stabilt mot hverandre mens noven på overstokken hugges. Foto: Henrik Jenssen.

Nå lages det jeg tror de uthugde flaten som var blitt igjen på Renmælmo-stabburet har vært. Det siktes ned mot understokken, og hugges en tilsvarende «liggeflate» på oversiden av overstokken. Denne flaten og sidene dens skal være litt mindre enn understokkens bredde på samme måte som tidligere, men også tredje stokk når den kommer senere. Her er det litt å gå på. Stokken kan roteres rundt underveis for å se om den ligger godt og stabilt. Det er mulig en må justere bredden på flaten noen ganger, og kanskje vinkelen på sidene, men i begynnelsen er det lurt å heller ta lite og prøve seg fram. Får en «liggeflatene» til å ligge godt mot hverandre blir de fine veiledere for det videre arbeidet.

Figur 10. Nå ligger stokkene mot hverandre og den tredje flaten som er et direkte steg i noven på undersiden av overstokken er hugget ferdig. Foto: Henrik Jenssen.

Når overstokken er snudd og den ligger stødig hugges en ny «liggeflate» på siden av stokken som nå ligger opp. Denne sikter en ned mot understokkens bredde, og hugger den dypere enn de forrige. Jeg bruker nesten å hugge den ned til 1/5-1/4 av stokkens høyde. Dette målet har mye å si for novens fasong, men kan justeres lavere senere. Det er fint å lage den sånn at den er i vater når «liggeflatene» under ligger godt mot hverandre, da blir den en fin referanse for at stokken ikke flytter på seg.

Figur 11. Her er det kinningene påbegynt. Foto: Henrik Jenssen.

Så hugges kinninger ut slik at de møtes i en linje ned mot senter av understokken. Fire viktige ting med kinningene er at man ikke bør hugge lengre ned enn halvparten av stokkens høyde (dette kan fort skje). Der hvor de møter «liggeflaten som er opp bør det være smalere mellom kinningene på hver side enn det en regner bredden på mosefaret vil bli. De bør være lange nok (i stokkens lengde retning) til at meddraget senere kommer til (her må en prøve seg fram, og
når en bra lengde er funnet kan det senere siktes ned mot kinningene på stokken under). Til sist bør flatene i kinningene i hvert fall være nokså plane. Dette sparer tid senere.

Så hugges det resterende av «liggeflaten» om til en egg hvor hver side går ned til bunnen av kinningene og skrår noe sammen. Her kan en igjen tenke at bredden nede skal være litt smalere enn bredden på mosefaret. Det er viktig at eggen kommer midt i stokken. Til dette arbeidet er det fint å ha en smal øks, f. eks. en hoggerøks, men om en ikke har dette kan et stort tappjern brukes.

Figur 12. Eggen på undersiden av overstokken er hugget ferdig, og stokken kan nå legges til side for øyeblikket. Foto: Henrik Jenssen.

Deretter løftes overstokken bort (den ligger fortsatt fint på liggeflatene sine) og kinninger hugges som tidligere på understokken. Så hugges «liggeflaten» dens om til en v-kløft. Det viktigste her er at kløften møtes i et punkt som er like nært, eller litt nærmere dit en vil overstokken skal felles til, som distansen den dype «liggeflaten» ble hugget til (1/5-1/4 av høyden på overstokken).

Figur 13. Nå er noven på over- og understokken hugget klar for meddraging. Foto: Henrik Jenssen

Nå bør allerede stokkene begynne å ligge ganske godt nedpå hverandre, men litt justering er nok nødvendig før det meddrages. En må egentlig bare se hvor det tar i noven, men noen av plassene som virker å være problematiske i starten er flaten på overstokken som ligger mot kinningen på understokken. Det er viktig her å hugge slik at innsiden av veggen kan bli i lodd.

På dette punktet tror jeg det vil være naturlig å markere og borre for dømlinger, men siden jeg ikke har plukket ned noen av stabburene jeg har undersøkt enda kan jeg ikke her si noe om hvordan eventuelle dømlinger er utført.

Når overstokken ligger godt nedpå og noenlunde i vater i lengderetningen må innerveggen loddes opp helt ferdig og overstokken festes. Det er viktig at overstokken ligger stabilt og ikke rører på seg mens det meddrages (jeg kilte noen killer i novene). Så kan det meddrages. Det er viktig å ha et meddrag som en kommer til i kinningene med. Dette kan som sagt justeres litt ut fra hvor lange kinningene lages, men det er også avhengig av type meddrag. Et med riss på begge sider fungerer ikke. Så stilles meddragshøyden til den høyeste stikkhøyden mellom over- og understokk, og en passer på å holde meddraget i vater. Så risses det langs stokken, og i novene sånn at det synes godt. Det er en fordel å slippe å tegne over med blyant etterpå fordi en blyantstrek blir som regel for bred.

Figur 14. Her demonstreres det hvordan man holder meddraget når man meddrager. Foto: Henrik Jenssen.

Så brukes en øks til å hugge ut mosefaret. Jeg liker at øksen er litt overskjeftet og at stokken ligger i en høyde fra midt på låret til hoften. Først hakkes fibrene mellom meddragsstrekene opp. Så hugges det rett ned på tvers av hakkene og langsmed stokken for å slå ut fliser. Så økses selve mosefaret ut. Det kan være lurt å ta det i to eller flere etapper før det hugges helt ned til streken. Det jobbes inn fra begge sidene av stokken og en hugger en «v-form». Det er viktig og følge med på fiberretningen slik at veden ikke river ut. Det er også lettere å jobbe med små hugg og langsmed stokken. Økseskaftet skal nesten jobbe 90 grader ut fra kroppen. Når det hugges etter meddragingen i novene er det viktig at flatene på overstokken som møter kinningen på understokken er en plan flate mellom begge sidene. Etter denne tømringen fortsetter ikke mosefaret ut forbi noven, men hugges flatt etter meddragingen både i over- og understokk.

Figur 15. Mosefaret er ferdig hugget ut, og noven er klar. Overstokken kan nå legges nedpå understokken og være tett. Foto: Henrik Jenssen.

Hvis alt er meddratt rett, hugget etter streken og stokken fortsatt ikke legger seg helt ned løser det seg som regel ved enten å hugge sidene i mosefaret brattere, eller «v-kløften» i understokken litt dypere. Mosefaret bør ikke bli for dypt, da er det bedre å hugge slik at det blir mer «u-formet».

Det er antagelig nå en bør bestemme utstikket i noven, vatre det opp, og sage rett.
Så hugges sidene på utstikket etter en mal eller et fast mål. Dette tror jeg er for å pynte hjørnene, og rette opp ujevnheter i stokktykkelse.

Når en nå skal begynne på neste stokk vil understokken allerede ha en «liggeflate» opp. Det er denne «liggeflaten» jeg tror har blitt igjen på stabburet hjemme på Renmælmo.

Figur 16. Stokkene ligger ferdig nedpå hverandre, men alle er ikke enda ferdig pyntet i endene. Foto: Henrik Jenssen.

Verktøyet jeg har brukt er fra venstre på bildet; vater, snekkerbile (øks), meddrag, og pjål. Tappjern ble også brukt litt, men er ikke avbildet.

Figur 17. Verktøyet som er brukt f.v.; vater, snekkerbile, meddrag og pjål. Foto: Henrik Jenssen

Arbeidsbeskrivelse av laft på stall frå Heimtveiten, Bykle Setesdal

Studentane har eit eige fag i tømring fyrste studieår. I faget har vi hatt ei vekes samling i Målselv tidlegare i år. Vidare har dei hatt ei heimeoppgåve der dei har kartlagt og dokumentert lokalt tømrarverktøy. Den avsluttande oppgåva i faget har gått ut på å lese gjennom ulike skildringar av arbeidsprosedyrer i tømring, vurdere desse, og vidare lage si eiga skildring av arbeidsprosedyre på ei nov dei sjølve arbeider med. Skildringa skal utformast med tanke på at ho skal ut på bloggen. Tidlegare har Jostein Utstumo skrive om flatlaft, Kai Johansen skrive om Trønderlaft og Sven Hoftun har skrive om Røsslinova. Studentane Henning Jenssen og Magnus Wammen har samarbeidd om å lage ein videofilm som viser arbeidsmåten dei har kome fram til i sitt arbeid med restaurering av stallen frå Heimtveiten. Her kjem introduksjon og filmen frå Magnus og Henning.

Henning og jeg har samarbeidet med denne oppgaven og vi sende inn en film som er klipt og redigert sammen til å sammenfalle hvordan vi har løst laftinga på stallen.

Stabbursnov frå Eggen gard. Et forsøk på å retømre Bardus eldste nov

Under samlinga i tømring i Bardufoss i februar var ei av oppgåvene tømring av 2 stk. prøvenover med utgangspunkt i novene frå stabburet på Eggen gard i Bardu.

Eggen nov 07 — Stabburet på Eggen gard er truleg eit ev dei eldste bygga som står att i Bardu. I enkelte kjelder er det og omtalt som eit loft.

Under dokumentasjonen og prøvetømringa av nova, synte det seg etterkvart at dei tre medlemmane på gruppa hadde noko ulike innfallsvinklar på arbeidet. Det vart ei lite tema i seg sjølv. Medan Henrik med sine arkitektgener teikna nova i ulike vinklar ut i frå våre observasjonar, så var Jens oppteken av å måle opp faste stader i kvar enkelt nov i kvart omfar i den nova vi studerte i andre høgda av buret.

Eg valte å fokusere på fotografering kombinert med å forsøkje å sette meg inn i korleis ein kunne sjå spor etter framgangsmåten i tømringa i den originale nova. Eg prøvde på eit vis å memorere den tredimensjonale nova, ut i frå å studere den og tenkje prosess for å få hogd dei ulike elementa. Samstundes tok eg nokre få mål, for å sjå etter mønster og faste dimensjonar i nova, men eg la lite vekt på detaljert oppmåling.

Eggen nov 06 — Nova vi studerte i andre høgda i buret, frå innsida. (nordvestre nova)

Vi fann få tydelege faste mål, og såg ikkje noko som tydde på at tømrarane på sluten av 1700-talet var opptatt av å gjere kvart enkelt omfars nov svært lik den førre.

Eggen nov 01 — Nova er svært utgliden, så det var ganske lett å sjå inni. Lysforholda var derimot ikkje egna for fotografering, og det blei tildels store kontrastar.)

Sjølv om novene særleg i andre høgda i dag er svært opne og luftige, skyldas dette nok over 200 års hard medfart av vær og vind. Eg oppfattar novene som svært godt hogne, og dei har nok opphavleg vore tette og fine å sjå til. Mitt inntrykk på synfaringa var og at dei såg ut til å vere som skapt for å formas med øks, og da kanskje berre med ei eller to for handa.

Eggen nov 02 — Verktyspor og novas form var tydelege.

Spor i kinningane tydar på at i alle fall ei øks som er bruka i tømringa hadde ein eggbreidde på om lag 4 norske tommar, ei slik øks kan nok i utgangspunktet vere tilstrekkeleg for å forme heile nova. Å ha ei noko smalare øks i tillegg ville nok vere greitt, men vi såg ikkje sikre spor etter dette.

Skisse Henrik — Skisse av nova for måltaking av ulike detaljar. Skisse: Henrik Jenssen

Denne nova er nært i slekt med tradisjonen frå Østerdalsområdet. Den kan kanskje beskrivas som ei form av østerdalsnov med tilnærma midtstilt femkanta hals og v-forma overhogg og tilsvarande spiss barke. Kinningane er hogne med ei nokså jamn lengde, omkring 4-5 tommar.

Eggen nov 05 — Utsida av buret, med dei fint tilhogne novhovudene.

Her er mitt forslag til framgangsmåte ved tømringa av denne nova, ut i frå observasjonar av originalen og tre dagar prøvetømring.

Hogge kinningar og overhogg i understokken.

En mulig veg kan vere å først hogge inn eit skår midt i der kinningane skal møtast. Dette er og midt i understokken, så det er greitt å sikte etter midten av den. Om ein hadde slått ei midtline på stokkane med sotsnor på førehand, ville det gjøre det lett å sikte inn midten av kinningar og overhogg. Skåringa gjør det lettare å hogge kinningane, og ein har midten av kinningane og botnen av overhogget klart for seg.

Kinningane trur eg ein tek etter det mål ein har bestemt seg for, og bruker deretter kinningane i stokken under som førebilete. I runde stokkar med noko varierande dimensjon vil kinningane nok kunne bli noko lengre på større stokkar. Om ein da ikkje ryr dei kraftigaste stokkane ned til passande dimensjon på førehand. Tømmeret i stabburet her var temmeleg jamntjukt, men dei grøvste stokkane var rydd inn til omkring same dimensjon som dei grannare stokkane.
Etter å ha hogge ut kinningane hogger ein ut overhogget, eit v-forma skår. Breidda på dette er eg litt usikker på korleis ein lettast bestemmer. Vi fant at ein måte er å ta det litt smalare enn breidda på overstokken, så ein er sikker på at ein ikkje havnar utafor stokklivet med underhogget. Djupna på dette varierte mye, men låg nok oftast innafor 1/3 av stokkhøgda.

Førebu overstokken

Her er det vanskeleg å vite kva for operasjon som har gått først. Ein løysning som eg syntes fungerte greitt var kappe stokken i rette lengda, og så bestemme kva side om er opp. Denne sida legg ein så ned, og merker opp midtline i endane med loddfjøl, og ein merker og opp dimensjonen på hovudet. Det er og god hjelp i å snorslå undersida etter midtlina. Novhovudene er hogne rette på stabburet. Sidan stokken er kappa i rett lengde, kan ein bruke eit fast mål frå novhovudet og inn til senter av nova. Så høgg ein kinningar ut i frå sentermålet frå enden av stokken, og så forma på novhovudet. Alt dette før stokken har vore lagt opp i veggen.

Eggen nov 13 — Overstokken ligg her opp ned. Kinningar og novhovudet er forma.

Felle stokken til medraging

Ein legg så stokken opp i veggen, i overhogget i understokken, i lodd og rett plassert i lengderetning.
No kan ein med passar måle opp avstanden ned til stokken under, og så bruke passar til å stikke opp både underhogget, og kor underkant av barken kjem.

Eggen nov 17 — Passar brukast til å stikke opp kinningar og barke.

Så snur ein stokken, og hogger ut underhogg og barke. For å finne breidda av barken mot halsen, kan ein bruke passaren som klave og måle breidda på overhogget den skal ned i.
Etter dette skal stokken i teorien falle ned og bli klar til médraging. Men etter eiga erfaring kan det hende ein blir nøydt til å finjustere litt for å får den på plass…

Médraging

Når stokken er komen så godt som ned til den under, kan den médras. Det gjekk å bruke same médragsjarnet til både å médra mellom stokkane og i kinningane. Men médraget vi hadde var ikkje heilt optimalt, og skulle ha hatt ein annan slip og vinkel.
Etter medraging høgg ein ut mosefaret, og ein høgg til streken i underhogget. Ein må og ta tilsvarande médragsmålet på barken. Så skal forhåpentlegvis stokken falle på plass.

Eggen nov 21 — Nova slik den er forsøkt retømra. Ikkje helt ulik originalen, men er framgangsmåten den same?

Verkty ein treng:

Øks(er). Vi brukte i hovudsak ei lita bile som var omkring 12 cm bred, samt ei skogsøks/ smaløks.
Loddefjøl (gjerne tilpassa breidda ein ønskjer på novhovudet)
Passer
Tommestokk (eller ein pinne med faste mål)
Médrag
Sotsnor

Per Steinar J Brevik 18. 3. 2016